Dear Users,
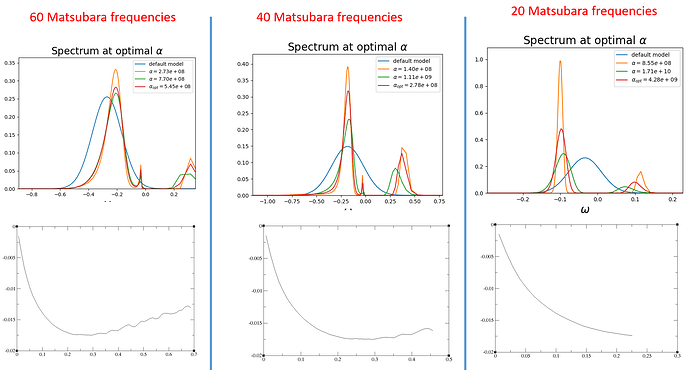
Can someone highlight the approximate number of Matsubara frequencies (MF) needs to be taken care for calculating spectral function using OmegaMaxEnt? Should it be just below the noise start in self energy plot? I have plotted three different scenario (please see the attached figure) for three choices of MF. Would the middle one be optimized choice as the blue curve (from default model) centers at the strongest peak and less noise data in self-energy plot?
Thanks for your valuable comment!
Regards,
Rajesh
Dear Rajesh,
Technically you need many more frequencies than that as you want to capture the tail. There should actually be a tail-fitting procedure to correct for the noise.
So more than few.
Olivier
Hi Olivier,
Thanks for the reply. As you can see for the other orbitals, noise started above 1.
At least up to 1, we can work with that, as it is almost close to tail. Could you please give some hint how to perform the tail fitting? Is it in OmegaMaxEnt?
Regards,
Rajesh
Hi Rajesh,
What DMFT solver are you using? The tail fitting is usually done at the solver step. The internal DMFT solver of ABINIT (dmft_solv 5) is supposed to do it automatically, while the TRIQS CT-HYB impurity solver has a few flags to set it up. It can also be done manually: you select a range of frequencies between 0.5 and 0.8 in your case, and fit the correct form for the self-energy, which is 1/iomega_n. Your blue curve is already noisy there, you could increase the number of QMC cycles for better resolution.
Best,
Olivier
Hi Olivier,
I am using dmft_solv 5. I have already dmftqmc_n 3.d9. If I increase to d10 then it says too many sweeps.
Regards,
Rajesh
There shouldn’t be a limit of the sweeps? But anyway, you have a good enough resolution for tail fitting. In any case, you perform the analytical continuation of the Green’s function no? Gtau? Then you should plot this quantity instead. It’s probably much less noisy. Gtau should be converged with frequencies.
Best,
Olivier
Hi Olivier,
I am doing k-resolved spectra and for that I am using “DS2Selfrotformaxent0001_isppol1_iflavor000x” file not Gtau for transforming into real frequency and analytical continuation.
However, increasing tolvrs from e-06 to e-07 and dmftqmc_l from 500 to 800 gives less noise.
I don’t know if increasing ngkpt will improve more or not.
Is there any indication from OmegaMaxEnt that analytical continuation is correct? If I change the number of frequency (e.g. 50, 70, 90) just below the noisy tail, I get some results but not confident if it correct or not!
Regards,
Rajesh
You should not cut frequencies. You can see from your results above that when you keep less frequencies, OmegaMaxEnt has more trouble finding the optimal alpha and gives a wider range of possible alphas, and so a broader range of different spectral functions. To check your results versus noise, you can analytically continue too iterations with different noise, it should be stable. Otherwise I would suggest to perform the tail fitting.
Best,
Olivier
Hi Olivier,
Thanks for the comments. I could not catch the last point about iterations with different noise! Could you please elaborate it?
Regards,
Rajesh
Dear Olivier,
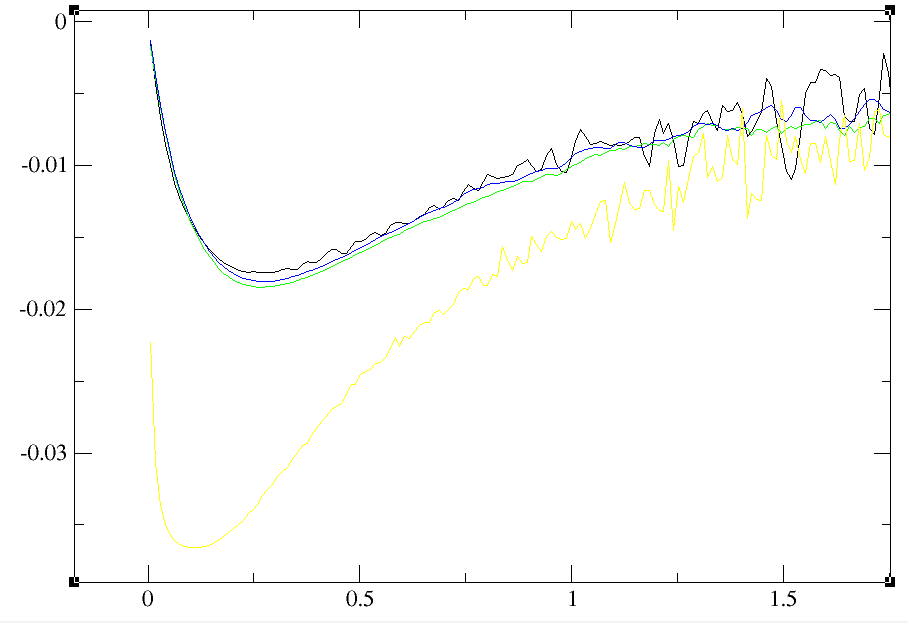
With increasing sweeps it improve the results. (see left side figure). I will try with more sweeps but time consuming!
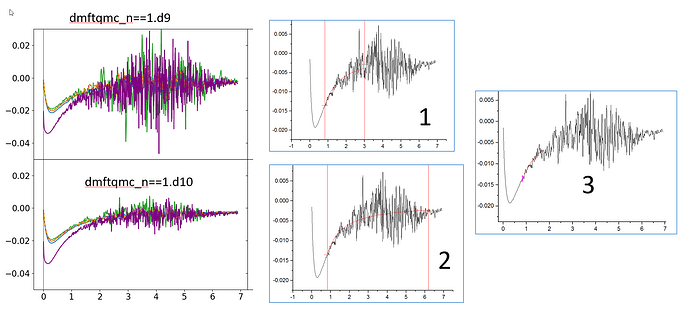
I also tried to perform tail fitting. Which range of frequency should be better, smaller one like in 3?
If I use the tail fitting data, do I have to give the data for OmegaMaxEnt up to the fitting range like 0 to 1.8 in case of 3?
Best regards,
Rajesh
Dear Rajesh,
My last point about few last iterations is that if you perform analytical continuation on these different iterations, the results should be stable, otherwise it means that either you are not converged, or that noise is making it different. It’s just a check that the noise is or not having major impact.
As for the tail fitting, I would say that the third option is sufficient. But once you found a fit, you should use it to extrapolate to larger frequencies.
Best,
Olivier