Comparison between collinear and non-collinear ferromagnetic magnetization using constrained

Running Abinit Ground state
1

Hi,

I was trying to get a picture of constrained magnetism calculation on simple cubic Fe lattice. What I did is the following:
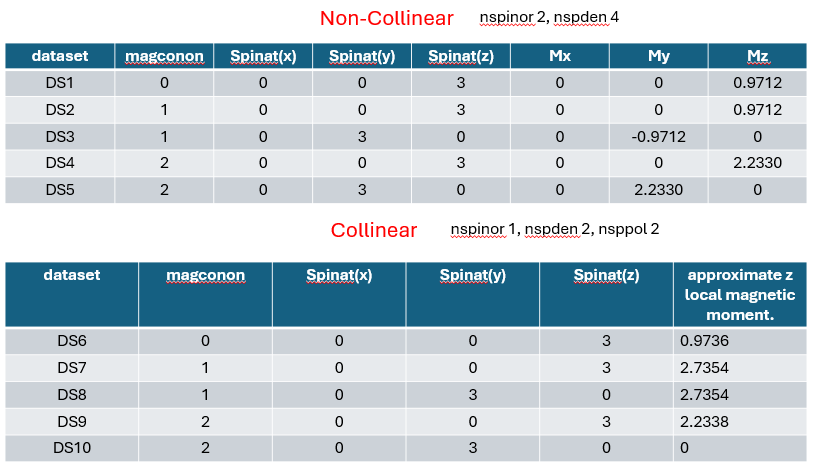
(1) Non-collinear calculation - 5 datase, with different combination of magconon and spinat.
(2) Collinear calculation - 5 dataset also with different combination of magconon and spinat.

Here, I attach the input and output file along with a summary of obtained magnetization.

I am concerned about the dataset DS3 and DS10. DS3 gives -ve magnetization while DS10 gives zero magnetization. I did not get why it gives such moments! Any idea please?

I understand from the documentation of magconon that for collinear case it is not vector treatment (nspden 2) therefore it does not give any components rather approximate local magnetic moment along z. My question is that is the magnetization really along z even when I initialized the spin along b-axis e.g. DS8 and DS10?

My 2nd question, can we treat collinear magnetism in non-collinear fashion to have components of moment along three direction? If yes, why the ferromagnetic system gives -ve moment e.g. in DS3?

Many thanks for your answer in advance!
Best,
Rajesh

summary
summary815×470 24.1 KB

Fe.abo (299.6 KB)
Fe.abi (1.8 KB)

2

Dear Rajesh,

I have a few remarks regarding your calculations:

1 - In collinear calculations, the x and y components of spinat are meaningless, only the z component is used. In collinear nspden=2 the magnetic moments are scalars and a direction in space is meaningless, and in Abinit the z value of spinat is used to specify the amplitude and sign of the scalar value. So, your collinear DS8 and DS10 calculations are not OK as you give a value on the y direction.

2 - You use getwfk -1, which means that for each calculation, you start from the previous WF file, which is not convenient if the previous calculation is with magnetization along z and the next one is with magnetization along y (as it is the case, e.g., for DS3 calculation which reads the DS2 WF). I would not use getwfk -1 in this case.

3 - You use a very low ecut and k-point grid, so, I guess it is for testing purpose only as those calculations are far to be converged and can give inconsistent results from dataset to dataset.

Best wishes,
Eric

PS: you can find some explanations/examples in this lecture on magnetism:

3

Dear Erik,

Many thanks for the video lecture and your explanation.

I realized that error later about the getwfk -1.

I understand that in collinear case the components of spinat are meaningless as it is a scalar and we can not specify the spin direction. Then, how can I calculate a collinear magnetic structure having spin along x or y direction instead of z-direction? Is there no way?

I am working on a system which is collinear magnetic with spin along z-axis. I wanted to check the difference in ground state energies when I take the in-plane spin (e.g. along x) and other with out-of-plane spin moment (along z) to prove the spin along z-axis is favorable.

Thanks,
Rajesh

4

Dear Rajesh,
There is a distinction between “physical” non-collinear/collinear magnetism definition and the one we used in DFT, I agree this is confusing…
If you want to distinguish between x, y and z directions, it is a “non-collinear DFT” calculation even if the magnetic moments are collinear in the physics sense. You have to activate the spin-orbit coupling and use nspden=4, nsppol=1, nspinor=2 and the spinat can be defined along x, y or z directions.
Best wishes,
Eric

5

Hi Eric,

When I try with nspden=4, nsppol=1, nspinor=2, it changes the lattice symmetry to lower one. I does not preserve the original primitive lattice. I have a rhombohedral (R-3m) unit cell and it becomes C2 (mC). Is it normal?

Thanks,
Rajesh

6

Dear Rajesh,
There is a limitation in the code right now for symmetries in non-collinear calculation that removes the improper symmetries when you have some, we are working on this limitation right now…
So the calculation is not wrong as it uses less symmetries than it should be, but it will be longer because of that. It can be problematic if you have an unstable phonon mode or an electronic instability in the symmetry you want to work with that the lower symmetry allows to relax, as your system will go to this lower symmetry phase if you relax, but if your system is locally stable under those symmetries it is OK (and it is the case in your system if Iḿ right).
Best wishes,
Eric