Dear community,
I have a question regarding the calculation of eph mobility.
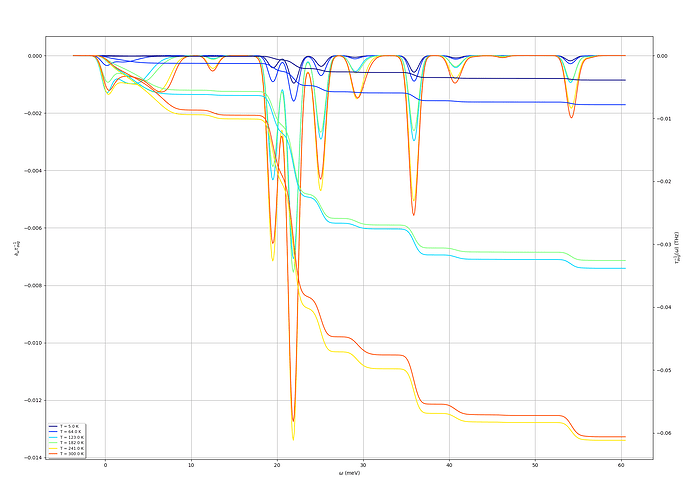
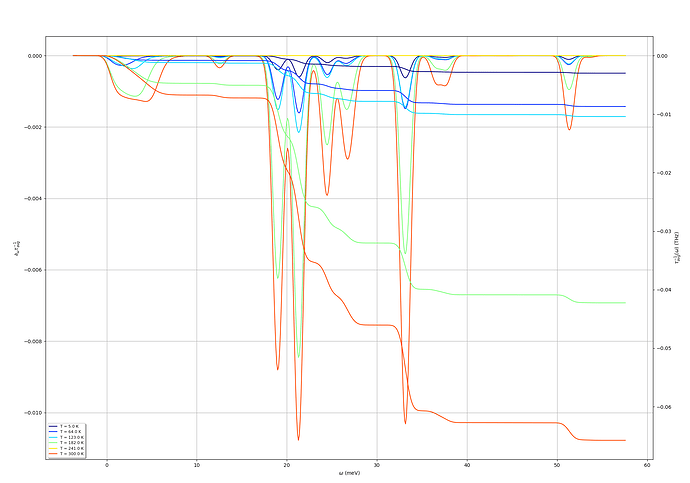
I would like to check the tau_{nk} with respect to phonon frequency ω.
My input file have following tags
eph_prtscratew 1
prtdos 1 # gauss method
tsmear 0.01 ev
dosdeltae 0.01 ev
eph_fsmear 0.01 ev
eph_intmeth 1 # gauss
zcut 0.01 ev # Lorentzian smearing parmeters
I use the sigeph.plot_scratew function from abipy’s sigeph module. Here, we obtained the derivative dτ/dω and the integrated τ curve. However, I noticed that there exists a small pocket of values when ω is smaller than zero. This seems unphysical, as there are no phonon states for negative frequencies.
I am unsure whether this is related to the smearing technique used in the calculation. Since I am studying 2D materials and Abinit does not support the triangular smearing technique right now, I used the Lorentzian method with a 10 meV smearing width. Is it possible to eliminate this small pocket, is there any problem for my calculation?
Regards,
Kongfer
Hi Kongfer
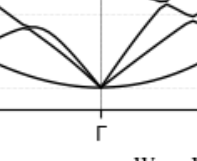
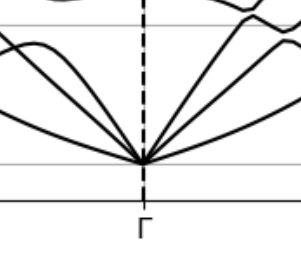
The peaks of your Lorentzians are positive, so it should be ok. 2D materials have issues with rotational sum rules and a parabolic mode which can easily go negative, but this is not your case.
The width of your Lorentzians is larger than the frequency, however, so the Dos like function you plot goes negative in omega. The q grid looks quite sparse from the number of peaks. Ideally you want to converge q and reduce the broadening to avoid negative Omega, but you can probably just truncate it. With the parabolic mode you will always have very low frequencies, so it’s delicate. Could also try tetrahedron with an extra artificial layer of q along z NxNx2
Hi mverstra,
Thank you for your quick reply.
Regarding the tetrahedron method, I have a 2D system with a large vacuum region and a degenerate conduction band at the bottom of the conduction band (CBM). Would it be suitable to use a k-point sampling scheme of N×N×2 after add another layer for this system?
I plan to reduce the smearing parameter to 2 meV and perform convergence tests. Additionally, I have employed equivalent k/q sampling, as suggested in the documentation, the q-point grid could be double or triple that of the k-point grid.
I also observed that applying tensile strain to the system causes the lowest phonon mode to harden (i.e., the slope of the phonon dispersion increases). Furthermore, the negative pocket of dτ/dω becomes smaller. I wonder if this behavior is related to the description you provided earlier.
An interesting fact is that when I use tetrahedron method, the output imaginary part of the electron self-energy (linewidth) is positive, while use Lorentzian technique this would be negative, it seems that the code behavior are different at the output stage.
This is well known: the parabolic band dispersion is only valid in the absence of strain.
For the sign of the SE this is strange indeed (the shape is relatively similar) - can you see something in the source code (abipy or abinit)? You are also plotting the d tau^-1 / d omega which is a bit different from the self energy alone. It comes straight from the abipy workflow? Are other quantities changing in sign as well?
After a quick search for abinit source code m_sigmaph.F90 (version 10.2.7), this is indeed a expected behavior, from line 2689 to 2693:
! TODO: Remove qint_method, use eph_intmeth or perhaps dtset%qint_method dtset%kint_method
! FIXME: Tetra gives positive SIGE2 while zcut gives negative (retarded)
! Decide default behaviour for Re-Im/Im
new%qint_method = dtset%eph_intmeth - 1
new%phwinfact = dtset%eph_phwinfact
Maybe it is just a notation difference.
Yes, the dtau^(-1)/domegra above comes directly from abipy. I haven’t observe other strange output until now.
I do not have a solid background in condensed matter physics, for Si and GaAs, it seems the band dispersion looks more sharp and is quiet different from parabolic shape. So it is materials dependent?
Ok, so it looks like everything is working as it should. See my previous response for the specificities of 2D materials. You have to decide what to do with the small (artificial) negative extension in omega, which is due to the broadening and very low freq due to the parabolic mode. Truncate, neglect, or converge the k/q and reduce the broadening.