K-points for (111) surface BZ

Running Abinit Ground state
1

Dear Abinitian,

Can some one share your experiences working with rhombohedral primitive unit cell and its superimposed (111) surface BZ representation like in this figure below?

I would like to know how I can obtain the coordinates of M(bar) and K(bar) in terms of rhombohedral primitive reciprocal vectors.

Thanks!
Rajesh
fig1

2
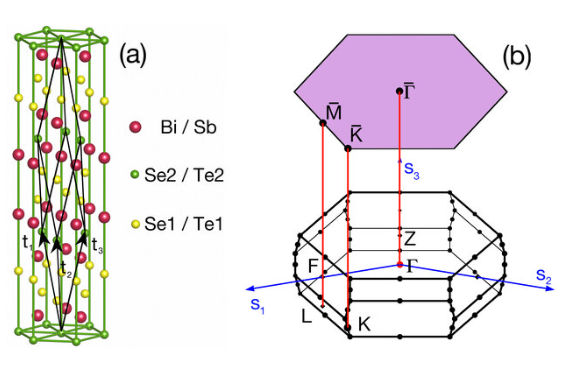
  1. I presume you are doing a rh cell calculation and want the bands along the G-M-K path, but with correct reduced k coordinates wrt the rh cell. You should go through cartesian coordinates to get to the correct rh kred:

K_{red}^{hex} = 1/3 \;\; 2/3 \;\; 0 (in your setting above, NB this changes depending on the real space angle you choose, 60 or 120 deg)

K_{cart}^{hex} = gprimd_{hex} * K_{red}^{hex}
where sprimd_{hex} is the matrix of the dimensionful reciprocal space lattice vectors for your hex cell

K_{red}^{rh} = gprimd_{rh}^{-1} * gprimd_{hex} * K_{red} = rprimd_{rh}^{T} * gprimd_{hex} * K_{red}^{hex}
where rprimd_rh are the real space lattice vectors t_{1,2,3} in the figure.
So you can calculate the transformation matrix A = rprimd_{rh}^{T} * gprimd_{hex} once and for all.

You do have to be careful about matrix transposing. Test it on a few points you know, or with the same matrices on in and output (just hex for example). Also be careful with the 2\pi factors which are sometimes introduced. Here they should all cancel from A. Abinit convention is no 2\pi in the rprimd gprimd vectors, they are added as needed for complex phases.

  1. getting the full surface band structure is another thing - you should accumulate all of the above energies for each k point in the plane above, but for varying kz_hex (which is orthogonal to the plane) i.e. same transformation matrix but with
    K_{red}^{hex} = 1/3 \; \; 2/3 \; \; kzred
    for kzred = 0…0.5 on a fine grid.
3

Hi mverstra,

Thanks for the useful hints. Is gprimed(hex) reciprocal lattice vector, you meant?

Rajesh